048-RNA-seq数据的基因共表达网络分析

Oct 24, 2018 7 min read cnposts

刘小泽写于18.10.24 最近开始写第一篇英文小论文，练练手，为将来写英文大论文做准备

蛋白互作（PPI）表示蛋白之间物理联系，它们几乎占据了细胞生物过程的中心位置。蛋白作为点，用无向的线连接
代谢网络主要表示生化反应，有助于生物生长、繁殖、维持结构。点是代谢产物，并用有向的箭头表示代谢过程或特定反应的调节作用
基因互作不同的点表示不同基因，描述它们功能相关性；可以根据基因的背景知识来推断线的方向
基因/转录调控表示基因表达是如何被调控的；点是基因或转录因子，它们之间的关系也是定向，例如Reactome、KEGG等数据库中表示基因调节的关系
细胞信号点表示通路中的物质，如蛋白、核酸或其他代谢物

1.2 Motivation for using co-expression networks

**看图说话：**某个细胞受到刺激1，也许它的A通路就会上调表达，B通路下调，结果可能比刺激前还要理想；

受到另一种刺激2后，A通路下调，B通路上调，那么可能就比较糟糕

通过共表达网络，就可以探索A、B通路是如何被调控的，以及背后基因的相互关系；另外，互作的基因一般都参与同样的生物途径

一般来讲，探索基因表达数据的标准流程是这样：

Differnentail expression analysis 想了解转录水平不同处理的差别背后的原因
Gene enrichment analysis (GO/KEGG) 得到差异基因，但是它们是干嘛的不知道，需要注释一下

但是有个弊端，它只能两两比较（如：感染与未感染），然后得到的结果也只是知道哪些上调哪些下调，是一个宏观的结论

使用Co-expression network 共表达网络可以分析多个处理的基因表达数据（例如：不同时间段处理），还能推断未知基因产物的功能、检测sub-groups

1.3 Network inference and reverse engineering

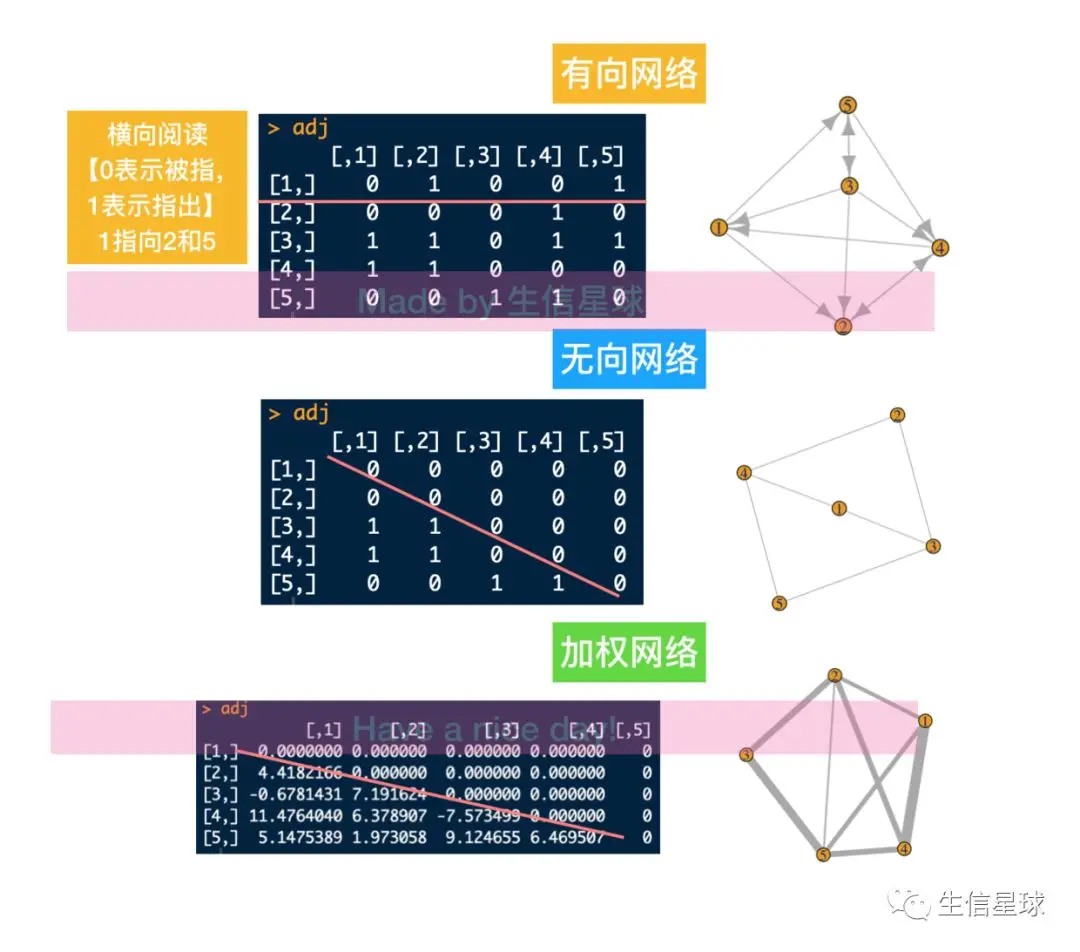
利用网络进行推断：可以使用表达量数据、已知的转录因子、ChIP-ChIP或ChIP-seq、时间序列等，因为网络是有向、交叉的，所以可以判断许多的关系信息

说到网络，就要看一下有向和无向网络：

install.packages("igraph")
library(igraph)
set.seed(1)
# 先构建一个有向网络临近矩阵

# create a 5x5 adjacency matrix
adj <- matrix(sample(c(0,1), 25, replace = T), nrow = 5)

# set diagonal to zero (no self-loops)
diag(adj) <- 0

# plotting with igraph
g <- graph.adjacency(adj, mode = "directed")
plot(g)

#再构建一个无向网络
adj[upper.tri(adj)] <- 0 #就是取矩阵的下半部分
g <- graph.adjacency(adj, mode = "undirected")
plot(g)

#再构建加权网络 weighted network
set.seed(1)
adj <- matrix(rnorm(25, mean = 3.5, sd = 5), nrow = 5)
adj[upper.tri(adj, diag = TRUE)] <- 0

# note that igraph ignores edges with negative weights
g <- graph.adjacency(adj, mode = "undirected", weighted = T)
plot(g, edge.width = E(g)$weight)

构建共表达网络的关键步骤：

数据预处理 Data pre-processing
数据转换、过滤或者均一化都会影响下游的分析
选择数据: 如果想了解整体调控关系，可以选择全部样本，因为它们中间会存在不同的扰动，更能体现共表达；也可以选择和某种表型相关的样本
过滤低表达基因 Filter low count genes
过滤低相关性/非差异基因 Filter low-variance/ non-DE genes ：这是构建Robust性能更强的网络的关键一步
数据转换 Log2-CPM：将RNA数据转换成更像芯片数据的类型
标准化 Normalization
临近矩阵构建 Adjacency matrix construction
step1: 得到相似性矩阵
既然目标是构建共表达网络，那么就要找到这个“共”所在，即找到基因表达量的相似性，因此需要用到一些寻找基因间相似性的算法
基因共表达分析中最常用的两种相关系数
皮尔森 Pearson correlation，是线性相关系数，反映两个变量线性相关程度。如果两个基因的表达量呈线性关系（数学上，线性相关指的是直线相关，指数、幂函数、正弦函数等曲线相关不属于线性相关），那么两个基因表达量的就有显著的皮尔森相关系性。Pearson相关系数适用条件为两个变量间有线性关系、变量是连续变量、变量均符合正态分布。同一量纲数据可以选择Pearson，例如mRNA表达量数据但在生物体内的许多调控关系，例如转录因子、小干扰RNA与靶基因，可能都是非线性关系，于是斯皮尔曼系数登场
斯皮尔曼 Spearman correlation ，是针对不同量纲计算的，比如两个通路看着相似，但其实单位不同，无法用pearson直接统计。无论两个变量的数据如何变化，符合什么样的分布，只关心每个数值在变量内的排列顺序。如果两个变量的对应值，在各组内的排序顺位是相同或类似的，则具有显著的相关性。
相关性|r|表明两变量间相关的程度，r为正表示正相关，为负表示负相关
step2 ：根据相关性分组
- 方法一：不管正负，按照相关性绝对值分组
- 方法二：只将正相关的基因聚在一起
step3 ：将“假相关“去除
- 方法一：利用sigmoid 转换：1/(1+e^-x^ )
- 方法二：利用power转换x^n^
检测共表达模块 Network module detection
利用聚类树（反映数据的关系强弱）
纵坐标反映了相关性，数值越低越相似，其实也可以看作是相关性的反义指标，因此蓝色的那一坨就表现特别相关

下面主要介绍前期数据处理部分，数据处理好了，后面真正的WGCNA才能做好

2.1 Preparing RNA-seq data for network construction

2.2 Prepare data and package

拿到一个数据，第一件事就是配置包

library('gplots')
library('ggplot2')
library('knitr')
library('limma')
library('reshape2')
library('RColorBrewer')
library('WGCNA')

然后读取表型和表达矩阵

samples <- read.csv('sample_metadata.csv')
raw_counts <- read.csv('count_table.csv', row.names=1)
dim(raw_counts)

大概的样子是这样：

加载注释信息

  library('Homo.sapiens') #加载物种注释，这里以人为例
  keytypes(Homo.sapiens) #查看注释包的内容，里面包含了各种的ID以及基因位置信息
  # 比如要匹配Ensembl的原始ID到gene ID，并且显示染色体信息以及基因位置
  gene_ids <- head(keys(Homo.sapiens, keytype='ENSEMBL'), 2)
  select(Homo.sapiens, keytype='ENSEMBL', keys=gene_ids, 
         columns=c('ALIAS', 'TXCHROM', 'TXSTART', 'TXEND'))
  # 就会得到类似下面的数据
  ## 'select()' returned 1:many mapping between keys and columns
  
  ##            ENSEMBL    ALIAS TXCHROM  TXSTART    TXEND
  ## 1  ENSG00000121410      A1B   chr19 58858172 58864865
  ## 2  ENSG00000121410      A1B   chr19 58859832 58874214
  ## 3  ENSG00000121410      ABG   chr19 58858172 58864865
  ## 4  ENSG00000121410      ABG   chr19 58859832 58874214
  ## 5  ENSG00000121410      GAB   chr19 58858172 58864865

Sample check

分析之前，看看样本质量如何，可以用热图或聚类

# 用热图
# add a colorbar along the heatmap with sample condition
{
    num_conditions <- nlevels(samples$condition)
pal <- colorRampPalette(brewer.pal(num_conditions, "Set1"))(num_conditions)
cond_colors <- pal[as.integer(samples$condition)]
  
heatmap.2(cor(raw_counts), RowSideColors=cond_colors,
          trace='none', main='Sample correlations (raw)')
}
  
#用聚类
{
    sampleTree = hclust(dist(cor(raw_counts)), method = "average")
    pdf(file = "pre-sampleClustering.pdf", width = 12, height = 9)
    par(cex = 0.6)
    par(mar = c(0,4,2,0))
    plot(sampleTree, main = "Sample clustering to detect outliers", 
         sub="", xlab="", cex.lab = 1.5,
         cex.axis = 1.5, cex.main = 2)
    dev.off()
}
  
# 如果发现跑偏的样本，除掉它
if(F){
      abline(h = 20, col = "red") #画一条辅助线,h的值自定义
  # 比如这里设置把高于20的切除
  clust = cutreeStatic(sampleTree, cutHeight = 20, minSize = 10)
  table(clust) # 0代表切除的，1代表保留的
  keepSamples = (clust==1)
  datExpr = datExpr0[keepSamples, ]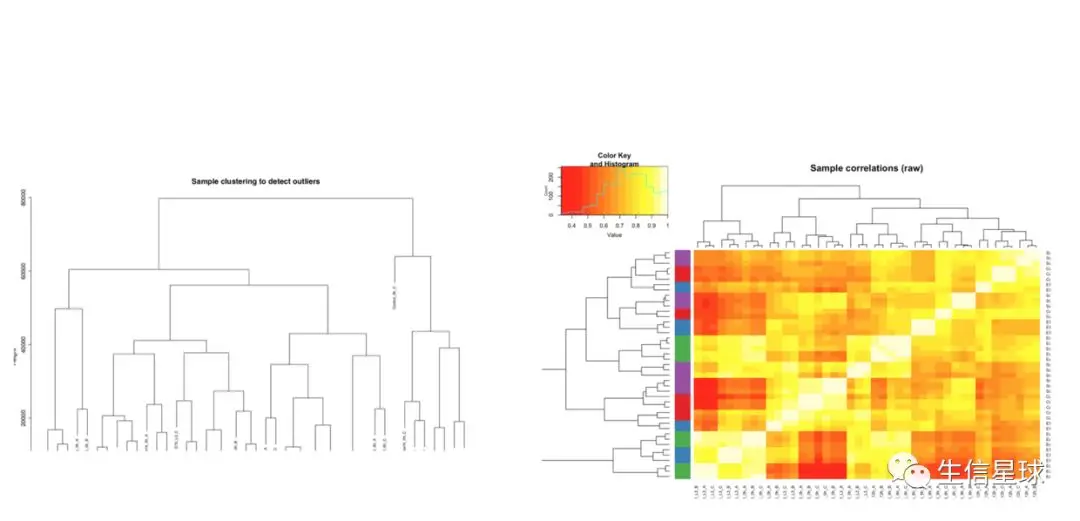
}

Low-count filtering 对样本质量满意后，我们只保留表达量丰富的基因，去除低表达量或者为0的基因

# 基因在每个样本中平均表达量为1就要被过滤
low_count_mask <- rowSums(raw_counts) < ncol(raw_counts)
filt_raw_counts <- raw_counts[!low_count_mask,]
sprintf("Removing %d low-count genes (%d remaining).", 		   sum(low_count_mask), sum(!low_count_mask))
  
#结果会返回类似：
## [1] "Removing 6154 low-count genes (14802 remaining)."

Log-transforming data

# 注意log使用要将真数+1 （真数就是这里的filt_raw_counts）
log_counts <- log2(filt_raw_counts + 1)
  
#然后画个图看看
x = melt(as.matrix(log_counts))
colnames(x) = c('gene_id', 'sample', 'value')
ggplot(x, aes(x=value, color=sample)) + geom_density()
  
#再画个热图
heatmap.2(cor(log_counts), RowSideColors=cond_colors,
          trace='none', main='Sample correlations (log2-transformed)')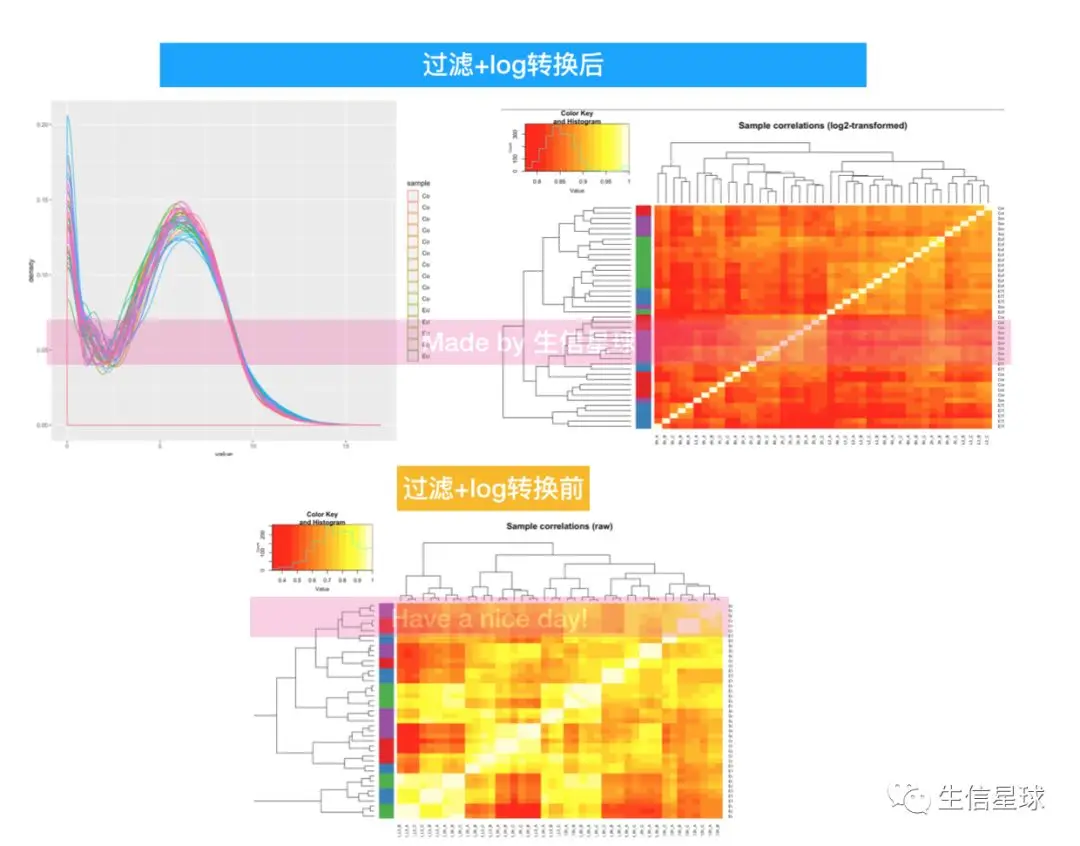

过滤并且log转换后，确实数据开始变好了

2.3 Remove non differentially-expressed genes

对于多个分组信息，需要生成几组两两组合的差异比较矩阵（取决于表型数据中的因子信息）；并且方差不显著的基因就要去除

这里需要了解的有 quantile normalization、 voom

# 首先，去除方差为0的基因，因为这些基因没有表现出任何差别，还有可能对下面构建模型产生误导
log_counts <- log_counts[apply(log_counts, 1, var) > 0,]

# 构建design矩阵为差异分析作准备
mod <- model.matrix(~0+samples$tissue)
# 如果需要考虑其他分组信息，只需要加进来就好
# 例如：mod <- model.matrix(~0+samples$tissue+samples$cellline)
# 再改一下列名（因为默认是把对应的分组信息全部当成列名）
colnames(mod) <- levels(samples$tissue)

fit <- lmFit(log_counts, design=mod)
# 生成一系列的两两组合差异比较矩阵
condition_pairs <- t(combn(levels(samples$tissue), 2))  

comparisons <- list()                                                                                                                                          
for (i in 1:nrow(condition_pairs)) {                                                                                                                                     
    comparisons[[i]] <- as.character(condition_pairs[i,])                                                                                                      
}   

# 设置一个储存差异基因的向量
sig_genes <- c()

# 为每对差异比较矩阵都生成差异基因，并存储到sig_genes空向量中
for (conds in comparisons) {
    # 这里conds如果中间有空格，就需要用make.names变成标准名
    contrast_formula <- paste(conds, collapse=' - ')
	# 然后就是标准limma流程
    contrast_mat <- makeContrasts(contrasts=contrast_formula, levels=mod)
    contrast_fit <- contrasts.fit(fit, contrast_mat)
    eb <- eBayes(contrast_fit)

#p值可以自定义，这里设置的比较严格
    sig_genes <- union(sig_genes, 
                       rownames(topTable(eb, number=Inf, p.value=0.005)))
}
# 最后把差异不显著的基因去除，留下DEGs
log_counts <- log_counts[rownames(log_counts) %in% sig_genes,]

WGCNA

048-RNA-seq数据的基因共表达网络分析

目录

1 背景 Background

2 共表达流程 Tutorial

1.1 Types of biological networks

1.2 Motivation for using co-expression networks

1.3 Network inference and reverse engineering

2.1 Preparing RNA-seq data for network construction

2.2 Prepare data and package

2.3 Remove non differentially-expressed genes

Yunze Liu

Bioinformatics Sharer

Related