116-StatQuest--在R中拆解PCA
刘小泽写于19.5.18 本文根据statquest视频整理,Josh讲解的很详细,于是我将这个教程整理出来,让更多的新手小伙伴了解
文章的所有代码在:https://statquest.org/2017/11/27/statquest-pca-in-r-clearly-explained/
内容总览
- 如何利用
prcomp()进行PCA分析 - 如何利用
base作图包和ggplot2作图包进行PCA可视化 - 如何计算每个主成分的离散贡献度
- 看看loading score
首先新建一个示例数据
新建一个10个样本,每个样本100个基因的表达矩阵,其中行为基因,列为样本
data.matrix <- matrix(nrow = 100,
ncol = 10)
然后给10个样本命名,用wt表示wild type(对照组),ko表示knockout(敲除基因的处理组)
# 列名
colnames(data.matrix) <- c(
paste("wt",1:5, sep = ""),
paste("ko",1:5, sep = "")
)
然后给100个基因命名
# 行名
rownames(data.matrix) <- paste(
"gene", 1:100, sep = ""
)
命名完了,再赋值
这种赋值方法可以学习一下:它是给100个行分别赋值,于是用了一个for循环,次数为100;然后每个循环中又要给10个样本进行赋值,前5个是wt,后5个是ko;rpois是创建泊松分布的数据,其中5是创建5个值,lamda是分布的均值,这个均值是sample从10到1000挑出来的一个值
for (i in 1:100){
wt.value <- rpois(5, lambda = sample(x=10:1000, size = 1))
ko.value <- rpois(5, lambda = sample(x=10:1000, size = 1))
data.matrix[i,] <- c(wt.value, ko.value)
}
看下数据
> head(data.matrix)
wt1 wt2 wt3 wt4 wt5 ko1 ko2 ko3 ko4 ko5
gene1 764 786 795 699 734 199 172 198 168 150
gene2 550 533 572 492 586 285 235 265 242 266
gene3 29 27 39 36 49 163 163 136 162 162
gene4 173 183 185 187 204 32 33 28 28 36
gene5 333 380 341 414 402 827 846 810 794 786
gene6 567 563 595 549 575 143 136 124 119 118
运行PCA
使用内置函数prcomp ,目的是展示样本相互之间相关还是不相关
pca <- prcomp(t(data.matrix),
scale = T)
这里要注意:prcomp函数是对行进行相互比较,但这里我们的数据行是基因,我们并不关心两个不同基因之间的差异或者说相关性,而是关心两个不同样本之间的关系,因此需要让样本为行,于是就需要转置t() (英文是:transpose)
然后这个函数计算结果返回三个东西:
x:它包含了作图需要使用的主成分信息(principle components)。一般作平面图就使用它的前两个PCs。 主成分怎么计算的?可以看之前整理的:https://www.jianshu.com/p/b83ac8f7f5a7
有多少样本就有多少PCs,x的结果就有多少列。比如我们现在有10个样本,计算结果就有10个PCs
sdev:standard deviation 标准差,利用它可以计算每个主成分在原始数据中占据了多少比例的离散度。
rotation:包含了PCA的变量信息,简而言之它记录了PCA使用的列的(也就是这里的基因)所占的权重
关于什么是loading可以看:https://stats.stackexchange.com/questions/72839/how-to-use-r-prcomp-results-for-prediction
作图
利用base包(利用x)
plot(pca$x[,1], pca$x[,2])

其中一个点表示一个样本,它的横坐标根据PC1确定,纵坐标根据PC2确定
可以看到左右两侧各有5个样本
每个主成分的离散贡献度(利用sdev)
也就是利用标准差求出来方差,然后算每个PC的方差占比,最后利用barplot可视化
pca.var <- pca$sdev^2
pca.var.per <- round(pca.var/sum(pca.var)*100,1)
barplot(pca.var.per)
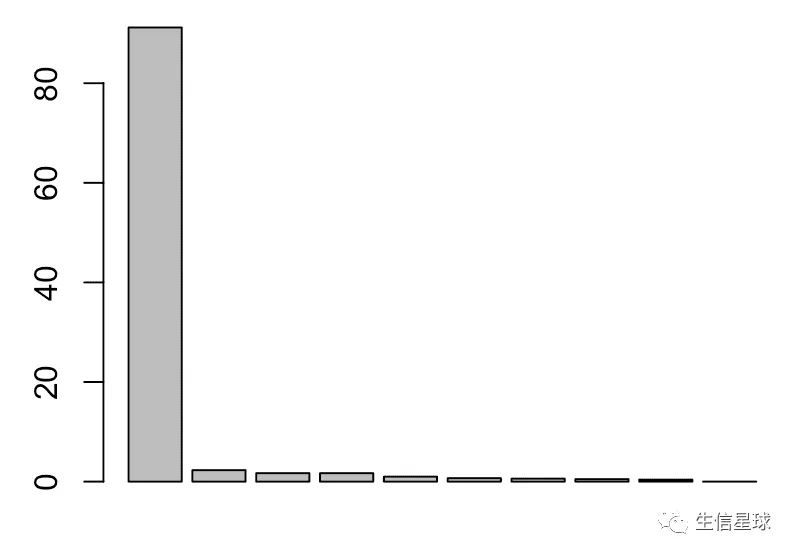
可以看到PC1对原始数据离散度的贡献最大,因此再看上面第一张图,从横坐标(PC1)就可以知道这两群差异很大
利用ggplot2优化
首先将数据整理一下:其中第一列是样本名,X列和Y列分别是各个样本的横纵坐标
pca.data <- data.frame(Sample=rownames(pca$x),
X=pca$x[,1],
Y=pca$x[,2])
> head(pca.data)
Sample X Y
wt1 wt1 -9.423527 0.1431157
wt2 wt2 -9.026152 0.1142019
wt3 wt3 -8.786758 -0.3014123
wt4 wt4 -8.766415 -0.7976410
wt5 wt5 -9.282003 0.7994244
ko1 ko1 9.205322 -0.8004204
然后画图代码
library(ggplot2)
ggplot(data=pca.data,
aes(x=X, y=Y, label=Sample))+
geom_text()+
xlab(paste("PC1 - ", pca.var.per[1], "%", sep=""))+
ylab(paste("PC2 - ", pca.var.per[2], "%", sep=""))+
theme_bw()+
ggtitle("My PCA Graph")
其中,首先指定了使用的数据:pca.data,然后我们要对其中的哪些进行操作呢?就使用aes()指定,表示x轴我要用pca.data中的X这一列,y轴用Y这一列,还想加个标签,用Sample这一列;
指定好数据后,geom_text用样本名代替投射点,这样就知道那个点表示哪个样本;
xlab和ylab分别设定了PC1、PC2在原始数据中的离散贡献值 ;
theme_bw()设定背景为background white;最后还设定了title
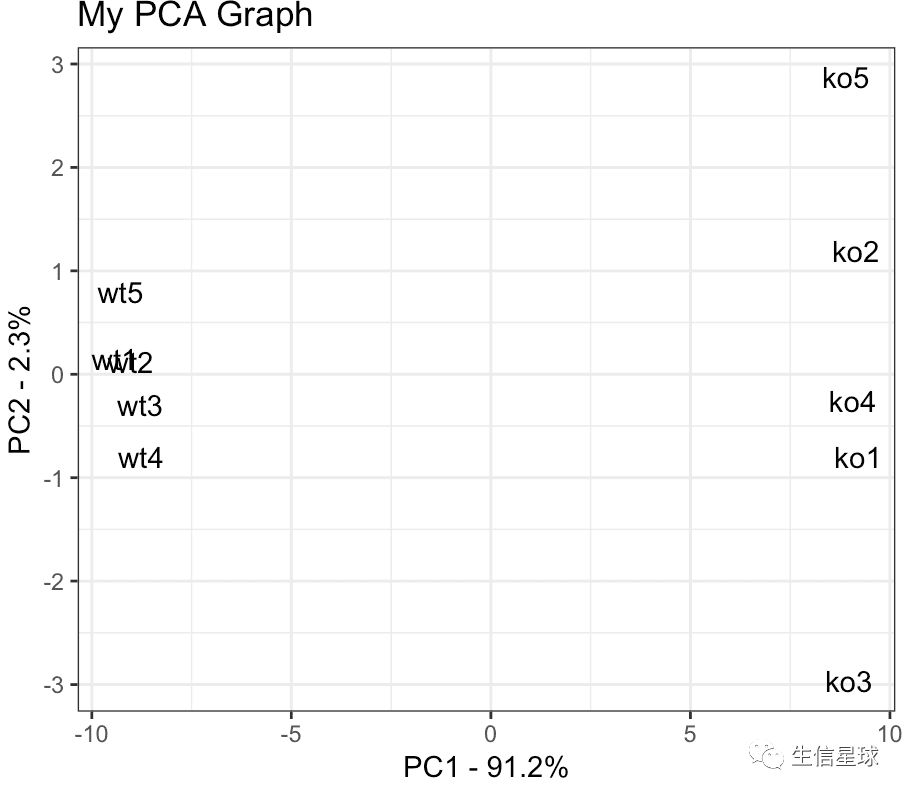
小tip:从上面的练习我们可以看到,PCA中展示了所有样本的差异,尤其是不同分组。虽然PCA已经做了降维,但是还是对于少量样本多个基因的情况。
但是数据也会存在大量样本大量基因,比如单细胞数据,动辄成百上千细胞一个测序样本,那时每个细胞就会被当成一个降维聚类样本对待,如果还是使用PCA的话,最后的降维效果也不好,于是就有了另一种方法:t-SNE。 之后会进行介绍,这里就当做是预告吧~
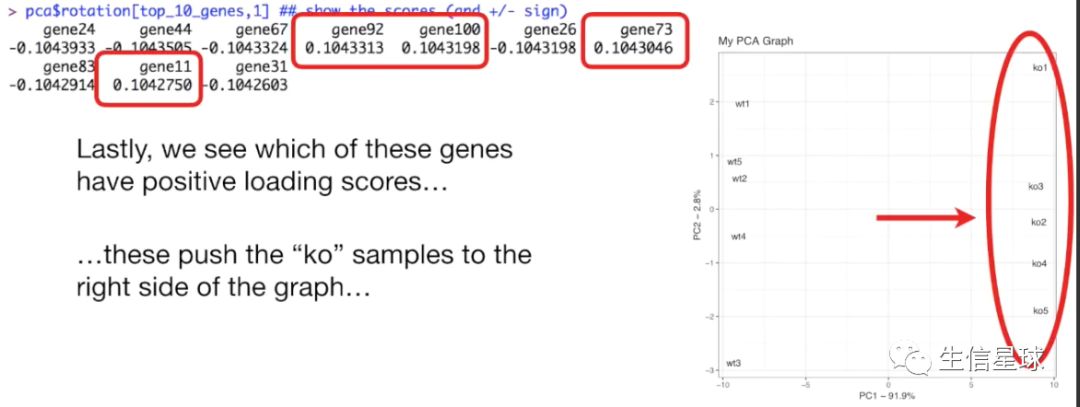
关于loading score
pca$rotation中存储了每个PC的变量的loading score,因为这里PC1是贡献值最大的,那么又是哪些基因导致了它的贡献值最大呢?
# 先取出PC1的loading score,也就是全部基因的权重
loading_socres <- pca$rotation[,1]
然后看上图,将样本推向左边👈的基因在其中的值为负数,将样本推向右边👉的基因为正数,因为对这两侧的"强推动"基因都比较感兴趣,于是取个绝对值,然后排序,取出前10个名字
gene_scores <- abs(loading_socres)
gene_socre_ranked <- sort(gene_scores,decreasing = T)
top10_genes <- names(gene_socre_ranked[1:10])
> top10_genes
[1] "gene95" "gene21" "gene86" "gene96" "gene79" "gene25" "gene74" "gene93"
[9] "gene17" "gene59"
最后,就可以看到其中哪些基因有正的loading score(向右推),哪些是负的(向左推)
> pca$rotation[top10_genes,1]
gene95 gene21 gene86 gene96 gene79 gene25 gene74
-0.1046586 -0.1046559 0.1046513 -0.1046302 0.1046266 -0.1046250 -0.1046122
gene93 gene17 gene59
-0.1046092 -0.1045993 0.1045802