109-Statquest-PCA学习
刘小泽写于19.4.27 聚类分析的基础就是PCA,掌握这个对以后那么这次就先跟着statquest来学习一下,视频链接在https://www.youtube.com/watch?v=FgakZw6K1QQ&feature=youtu.be>
好的,首先看看为什么需要进行PCA?
假设现在有一个表达矩阵,行为基因,列为样本,中间数据是表达量:
先假设有1个基因,在6个样本中存在
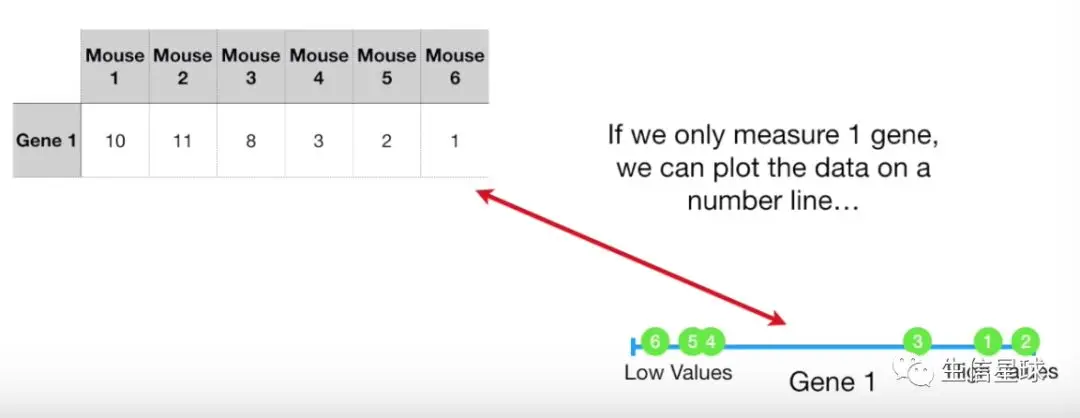
把这6个表达量都显示出来,可以在一条直线上绘制出高表达和低表达(可以看到1,2,3更接近,并且高于4,5,6)
再加1个基因,还是6个样本中存在
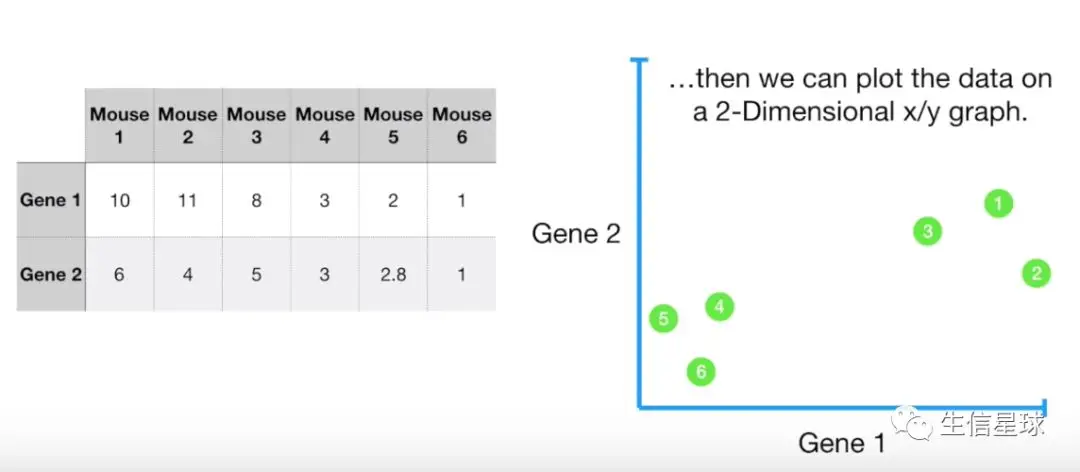
构建了一个2维空间,基因1的表达量可以用横轴表示,基因2用纵轴表示。可以看到在基因1、2的作用下,样本1、2、3聚集在右上角,4、5、6聚集在左下角
如果3个基因呢?
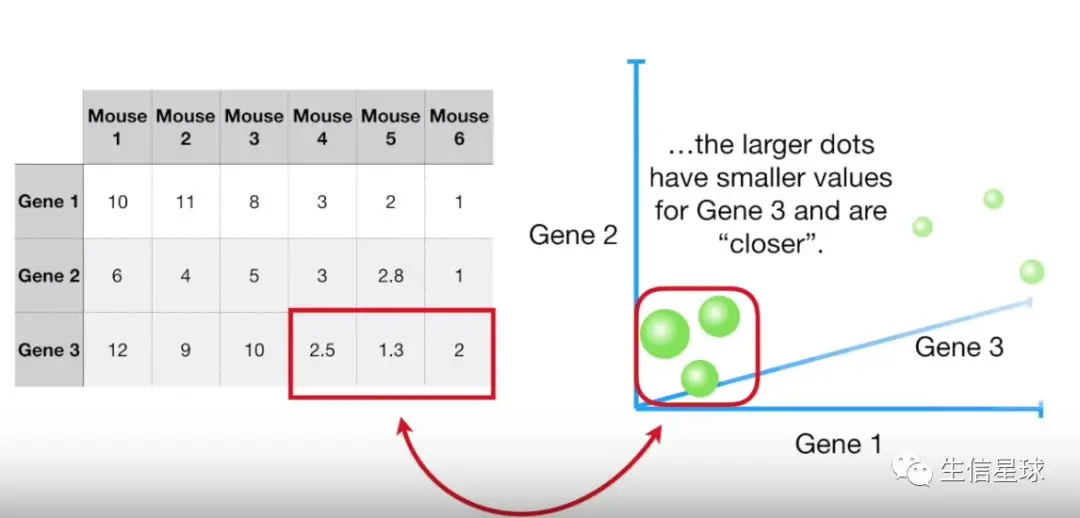
就构建出了3维空间,点越小意味着数值越大,离得越远
但是,如果是4个基因,我们就无法画出数据了,因为需要4维空间
因此,PCA的作用就是:对超过4维的数据降维到一个2D平面图中,并且这个图中”相似相聚”
PCA怎么操作的?
还是利用2维(2个基因)的数据进行理解:
- 先得到Gene1的平均数(横轴红色)
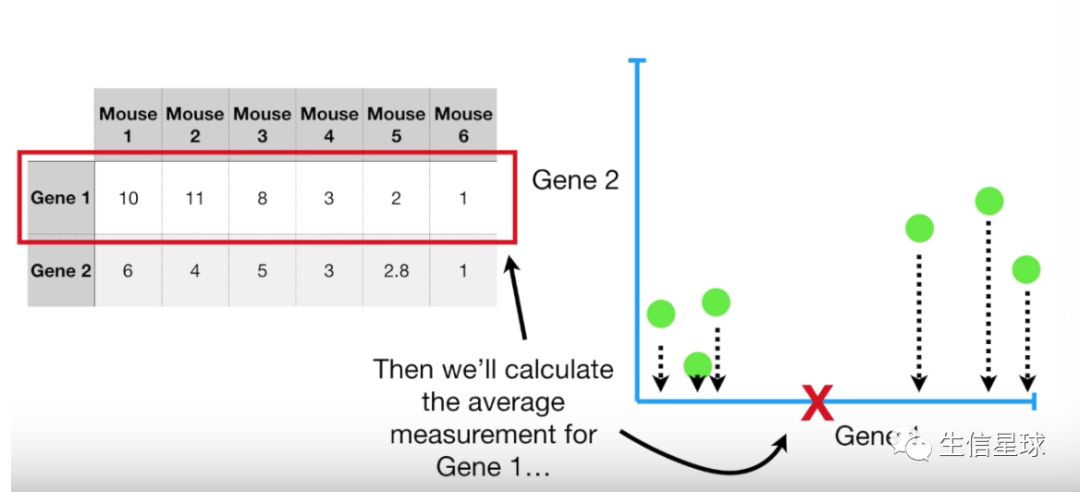
- 同理得到Gene2的平均数(纵轴红色)。
- 接着计算整个数据的中心:(蓝色)
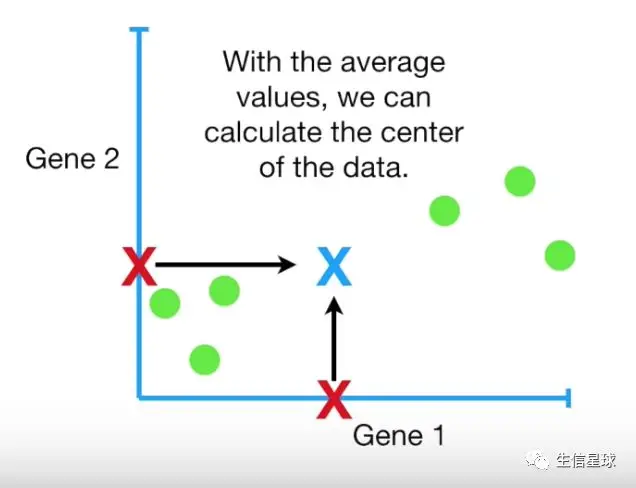
- 然后将数据平移,保证最后的中心在(0,0)的位置
这里注意:数据平移并不会改变数据结构以及相互之间的大小关系,比如原来最大的值现在还是最大;原来在最左下方的现在还是在那个位置
平移后的数据可以做一个辅助线进行拟合。先随便画一条穿过中心点的线,然后进行旋转,尽量拟合进来最多的数值。
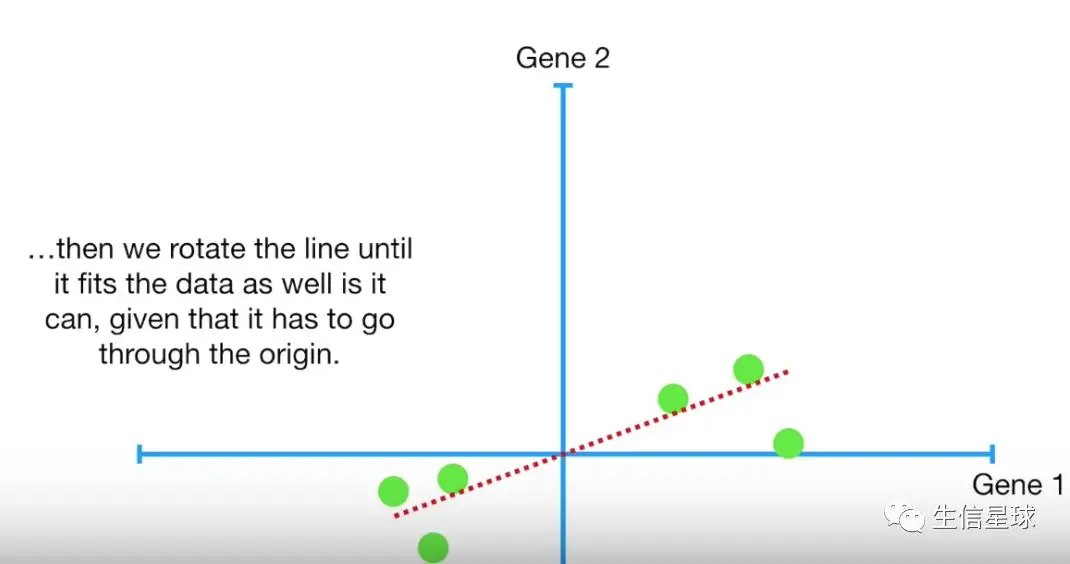
这里又引入一个问题:PCA是怎么判断哪条拟合线质量最好呢?
比如随便画一条,然后将数据投射到这条线上,它看的是投射点到原点/中心点(0,0)的距离平方
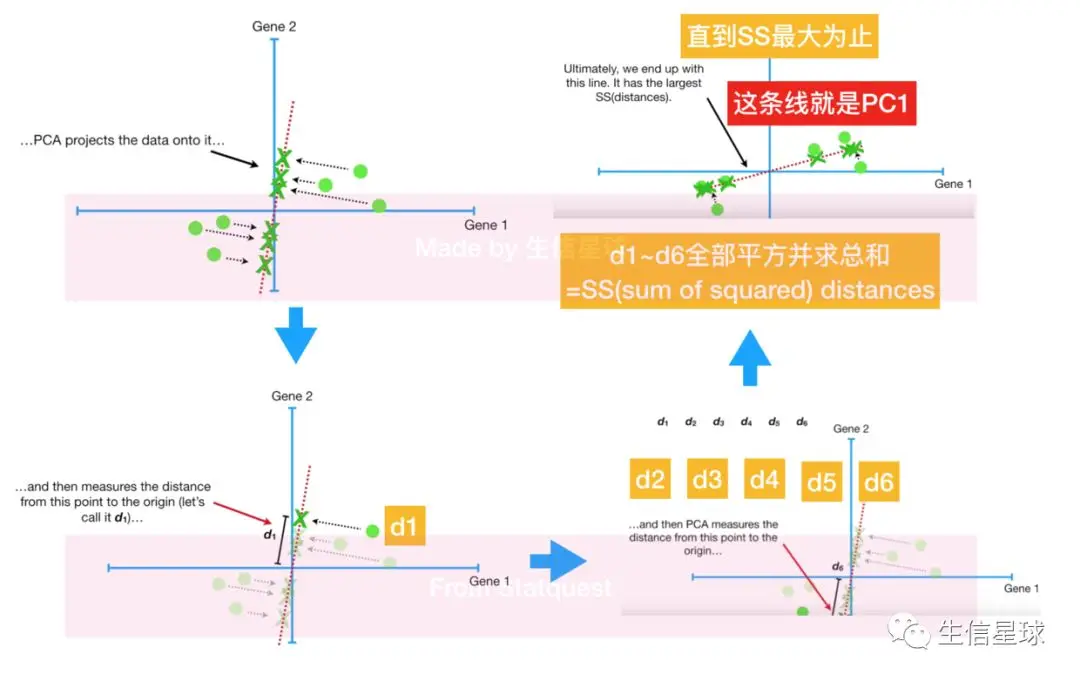
得到了PC1这条拟合线,假设斜率为0.25,就意味着:沿着x轴走4个单位,才沿着y轴走1个单位(术语叫做:Gene1和Gene2的线性组合=> linear combination)。换句话说就是数据主要是沿着Gene1的x轴分布,数据整体分布受Gene1的影响更大
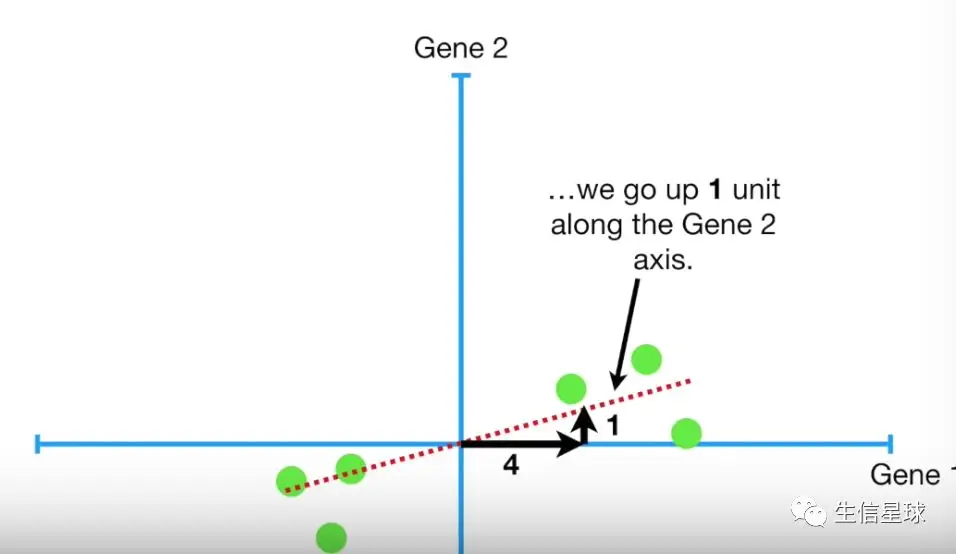
因此,当看到"PC1 is a linear combination of variables”,意思就是PC1是由几种Gene1成分加上几种Gene2成分组成的
确定了PC1后,进行scale缩放操作,将红线长度缩放成1,其他两边也进行等比例缩放。【术语:0.97的Gene1与0.242的Gene2叫做PC1的"Singular Vector"或者"Eigenvector”】 ,然后Eigenvector再开方得到的结果叫”Singlular Value for PC1”
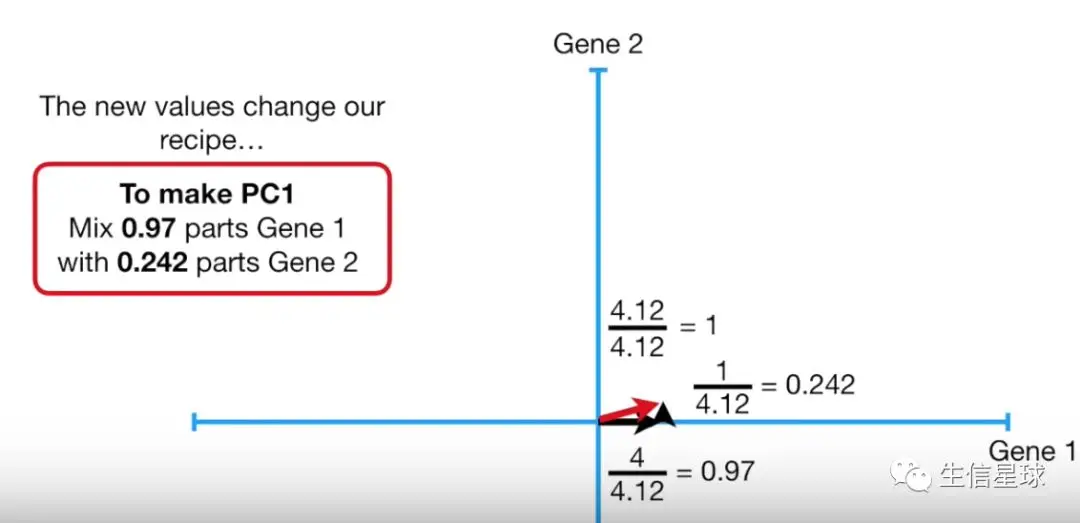
因为这是一个2维的图形,因此PC2是PC1的垂直线,并且不需要任何进一步的操作
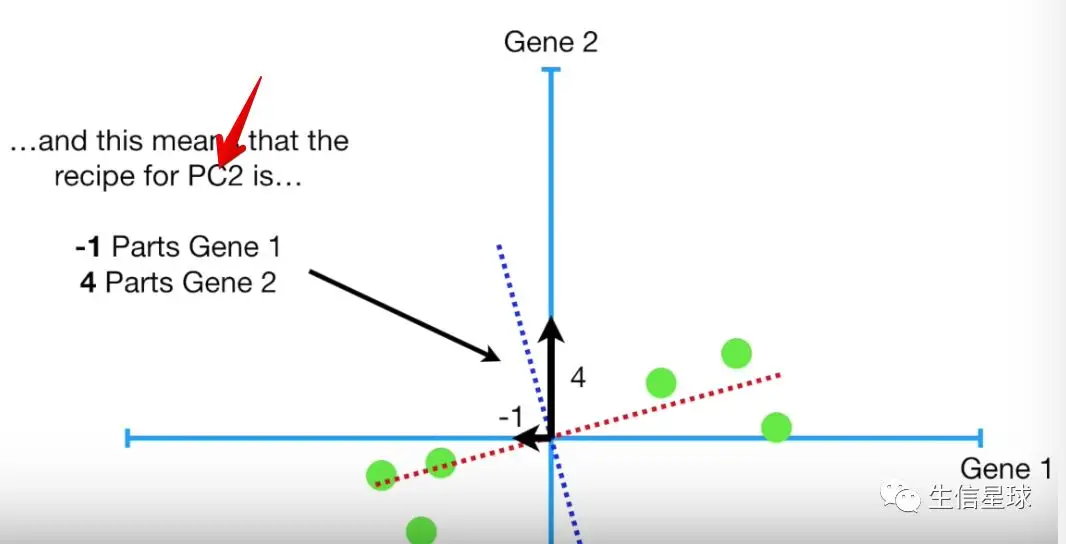
然后就是画最终的PCA plot
首先就是将PC1放到水平
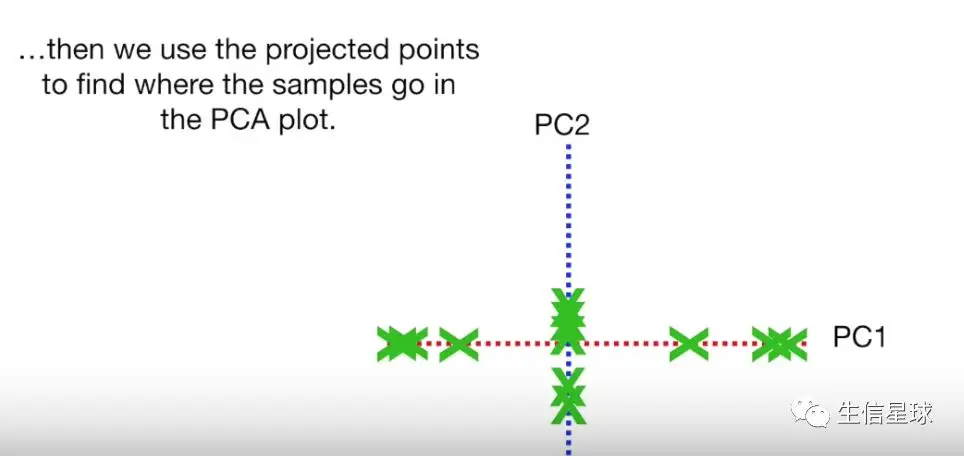
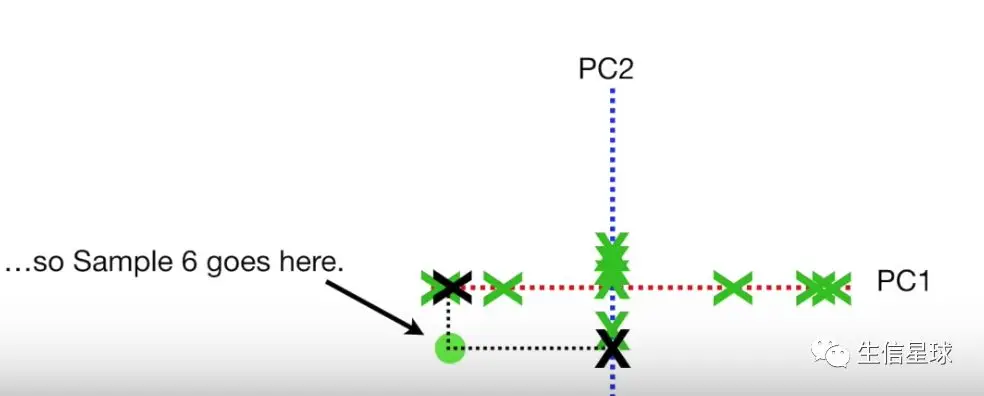
接着找到PC1、PC2同一个投射点在2D图中的位置,比如Sample6
计算PC1、PC2的贡献率
先分别计算PC1、PC2的variation,然后算比例即可

总结
对于简单的二维数据,很方便理解,n维数据也是这样处理,大体思路就是:
计算n个维度(或者说n个基因)的均值,找到数据中心
中心平移到(0,0)
找到跨过中心点的最佳拟合线=》PC1=》有n个组成成分(例如:0,62 parts Gene1; 0.15 parts Gene2; 0.77 parts Gene3,其中Gene3 is the most ingredient for PC1)
找到垂直的PC2,同样n个组成成分 。。。
最后找到PCn,它与前面的各个PC都垂直
PC1放到水平,然后根据PC1~PCn中同一个sample画出交点 (因此这也说明了为什么通过PCA可以看批次效应:因为PCA图中的每个点都是一个sample,这个点中包含了大量的表达量信息;如果说本来生物学重复的sample在PCA图上离得很远,那么就意味着它们的表达量差异很大,这是不符合实际的,因此可能存在批次效应)
根据每个PC的variation计算贡献率